每当我们在玩游戏时，不禁发问，图像是如何显示的呢?如何将一个三维物体显示在二维的屏幕上，这也就是视图变换(Viewing Transformation)所做的事，以下是基于我自己的理解的简要概括。

视图变换(Viewing Transformation)

视图变换(Viewing Transformation)可以分为四个步骤，即相机变换(Camera Transformation)以及模型变换(Model Transformation)，以及之后的投影变换（Projection Transform)以及视口变换(Viewport Transformation).由于通常将第一步第二步并称为”模视变换“(ModelView Transformation)(引号的原因是笔者自己也不确定这是否有准确的译名）。那么下面进行分步骤概述。

”模视变换“(ModelView Transformation)

首当其冲的自然是相机变换(Camera Transformation)，在讲之前我们需要定义下面几个东西。

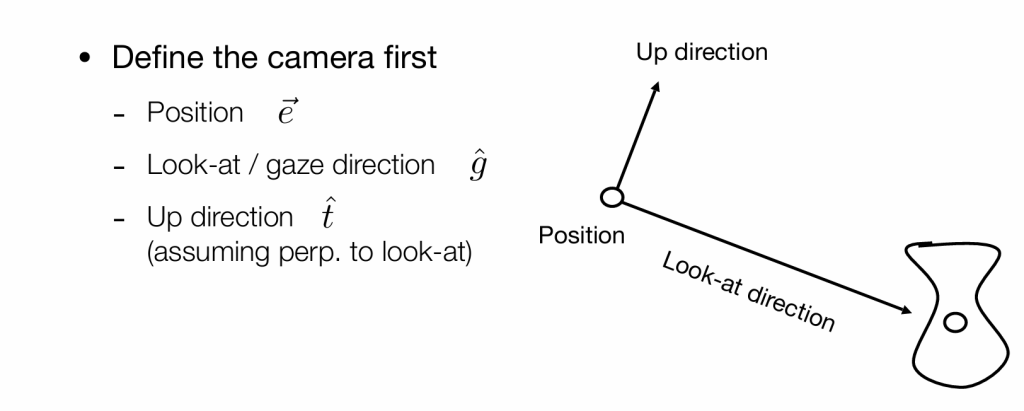
我们使用三个向量来定义一个相机，(即我们在3D世界观察物体的视点，在换句话说就比如人类的眼睛）用向量e代表相机的位置(Position),向量g代表注视方向(Look-at/gaze direction),向量t代表向上的方向(Up direction),为什么要这样定义呢，这实际上就是在给相机自身建系，而我们想要得到的结果就是将相机移到世界坐标原点（约定俗成），那么所以我们要做的就是先将向量e平移到原点，然后将向量g移到世界坐标-z轴,将向量t移到世界坐标y轴，然后对向量g和向量t进行叉积即可得到要移到x轴的对象。(叉积得到的是与两个向量垂直的向量),也就是如下图所示

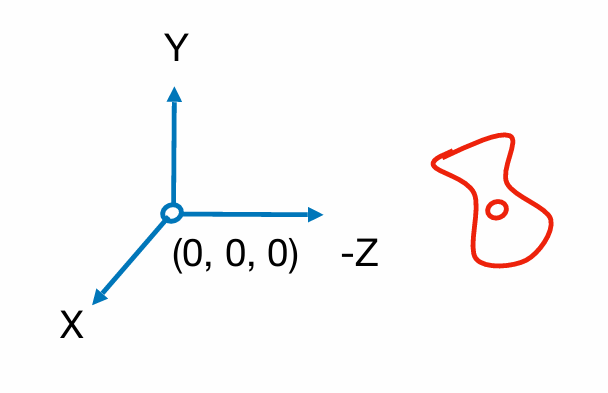
至于为什么是-z，是因为这里用的是右手坐标系，此时转换到-z是更合理的，如上图所示便知。而之后的第二步所谓的模型变换(Model Transformation),也就是应用相同的变换，保证所看的东西不发生改变。那么接下来，我们要通过怎样的数学计算来实现呢？

答案是——矩阵，如果你学过线性代数的话，一定知道矩阵跟向量是可以互相转换的，向量可以写成矩阵的形式，那么自然我们也可以用过矩阵的乘法实现向量的变换。那么接下来就出现了一个新的问题，我们应该用什么矩阵来描述这一复杂的转换。为了方便理解，我们可以分步进行操作。

如上图所示，他无外乎是两种变换——平移和旋转，平移矩阵我们很容易就能得到，如下图所示：

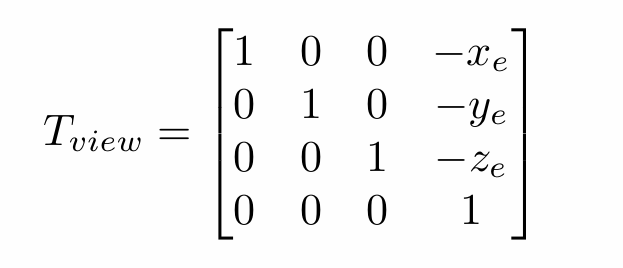
如果你问为什么要用四维矩阵，是因为在向量运用矩阵转换时，如果采用三维矩阵(三维向量），平移将作为一种特殊情况处理，而我们加上一维，便能统一运算，只使用一个矩阵就能实现这些变换(而应用这个的点的坐标我们叫做齐次坐标)。那么接下来就是旋转矩阵，显然直接写这个矩阵并不是那么好写，因为他是从三个且三维都有值的向量出发的，那么此时我们运用一个性质，旋转矩阵的逆矩阵等于它的转置，他理应作为一个旋转矩阵自然也有这个性质，所以我们利用这个性质可以反过来从原点出发，变成将-z移到向量g,将y轴移到向量t，于是乎我们就能得到一个旋转矩阵的逆矩阵，再求转置就得到了我们所需要的旋转矩阵，如下图所示：

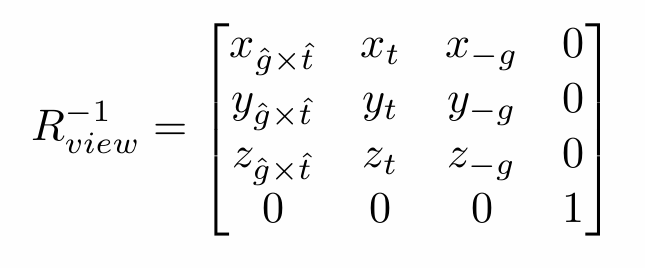
先左乘平移矩阵再左乘旋转矩阵，即可得到相应的转换，至于模型，正所谓相对运动，我们要保持物体不变，那么自然也要讲物体运用相同的矩阵进行转换，从而达到不变的效果，至于运动的物体，本篇不会提及。以上便是”模视变换“的大概内容。

投影变换（Projection Transform)

在投影变换中，我们所要解决的便是将三维物体进行进一步处理，为最后的视图变换做准备，它也分为两个步骤，分别为正交投影(Orthographic Projection)以及透视投影(Perspective Projection).这两者简单区别就是前者得到的物体相对大小位置不会变化，而透视投影则会发生变化，遵循”近大远小“的原则，如同现实一样。具体而言，正交投影将物体变成一个边长为1的在原点的立方体(cuboid)，随后的透视投影让物体最终效果更加符合现实。那么具体步骤如何如下：

首先进行的是透视投影，之后我们要将原本透视投影的物体得到的视锥(frustum)转换成一个立方体（cuboid),这要怎么操作呢？我们首先给出两个3D物体的形状。

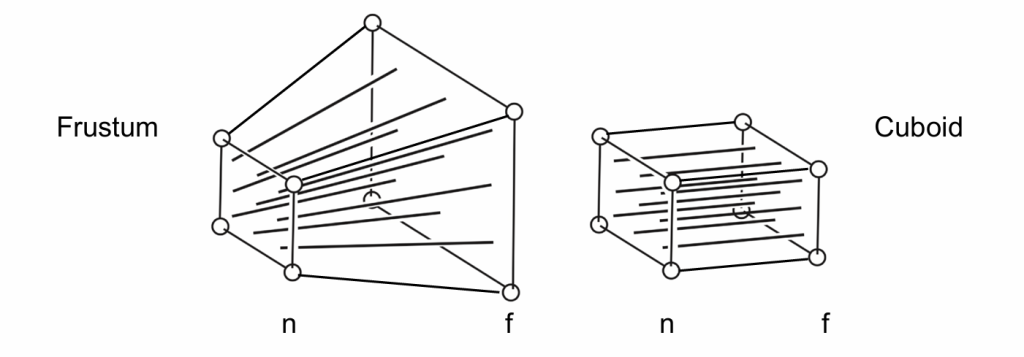
这要如何转换呢。答案很简单，我们只要把最后那个面压缩到跟前面那个面一样就行了，那如何实现呢？我们不妨用侧面图观察：

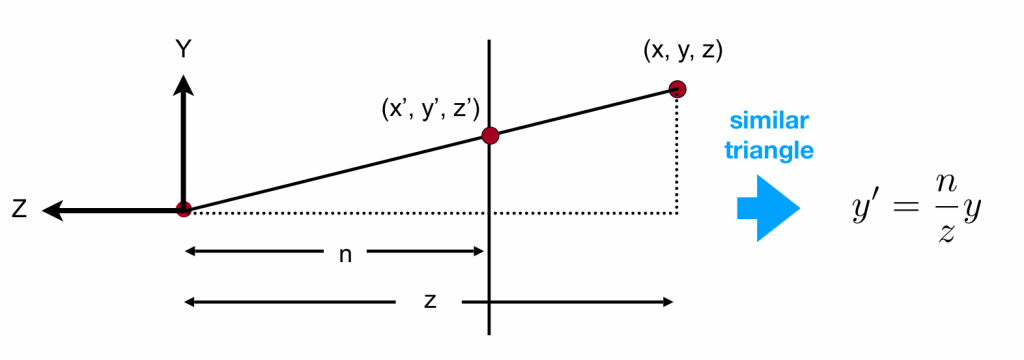
这里可以得到我们只要将y点坐标变成n/z*y就行了，此时我们运用一个齐次坐标的性质，(1,0,0,1)与 (k,0,0,k)表示同一个点。所以，我们可以得到我们的目的坐标为：

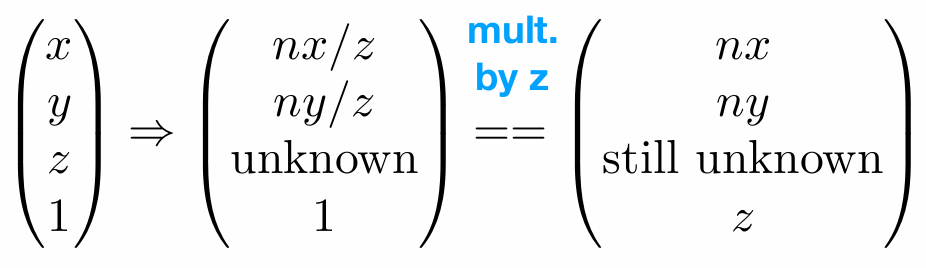
进而求得相应的变换矩阵为：

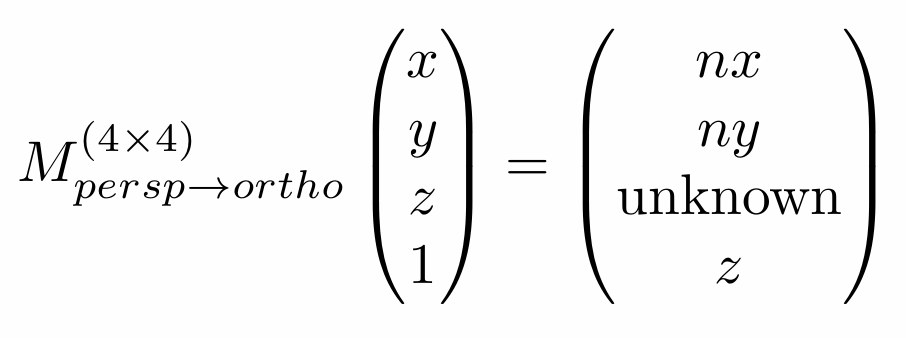
由于我们不知道z如何变化对应矩阵我们也无法写完，那么如何求出具体转换矩阵呢？

答案是约束条件，之前我们说过他的定义是将最后的面压缩到跟前面的面一样，那前面那个面的z坐标应该不变才对，因此我们可以得到：

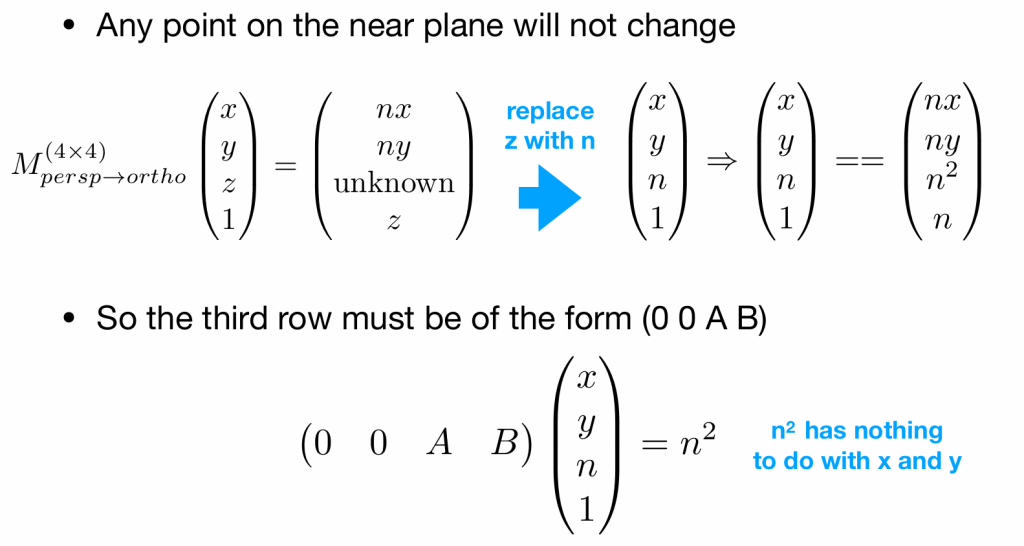
由此我们可以得到An+B=n^2。同理我们可以得到最远面的z轴坐标在变换过程中也是不变的，因此：

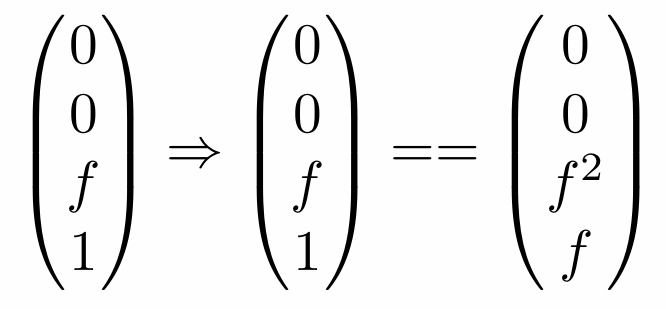
将上述两式联立即可求出A，B的值分别为A = n+f,B= -nf.从而求得转换矩阵为：

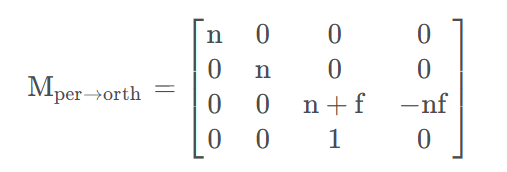
那么接下来进行正交投影(Orthographic Projection)，上文说到正交投影是将物体变成在原点的边长为1的立方体，那么其转换矩阵也显而易见为：

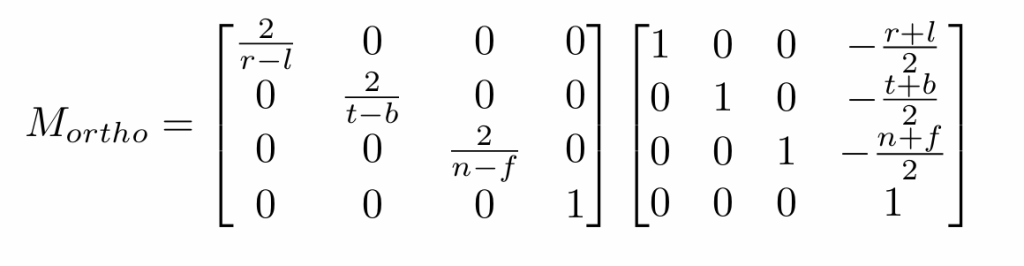
之后依次左乘矩阵得到总变换矩阵为：

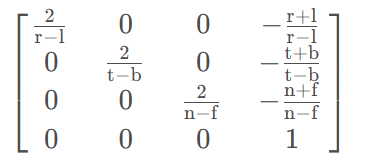
以上便是投影变换(Projection Transform)的全部内容

视口变换(Viewport Transformation)

在经过前面的MVP(即Model,View(Camera),Projection)变换之后，我们就要真正将三维物体转换到二维了。再讲具体变换之前，我们先定义屏幕空间，它的宽为width,它的高为height.那么实际上我们只需要把Z轴先丢掉(之后会做进一步处理),然后将此时边长为1的正方形缩放至[width,height]的屏幕空间。但由于一开始物体在原点，所以我们先要对他进行平移操作到屏幕中心，再进行缩放。以下是最终得到的矩阵：

最后再左乘这个矩阵即可完成变换，实现三维到二维的转换。

下一个打算跟着课程讲解光栅化的具体流程，光栅化说白了就是得到二维图形如何具体显示以及其中出现的问题及其解决方案，这些将在下一节提及。

本文图片来源：

1.GAMES101-现代计算机图形学入门-闫令琪 Lecture 04 Transformation Cont._哔哩哔哩_bilibili

2.(27条消息) 计算机图形学二：视图变换-Viewing-Transformation_西电卢本伟的博客-CSDN博客